Acrobot

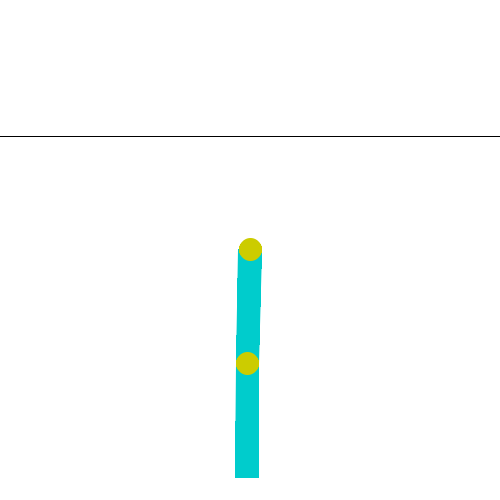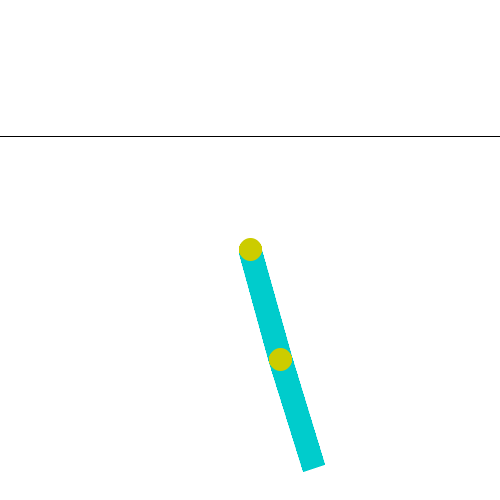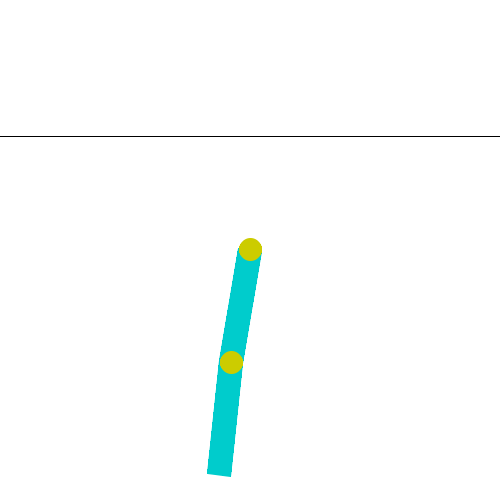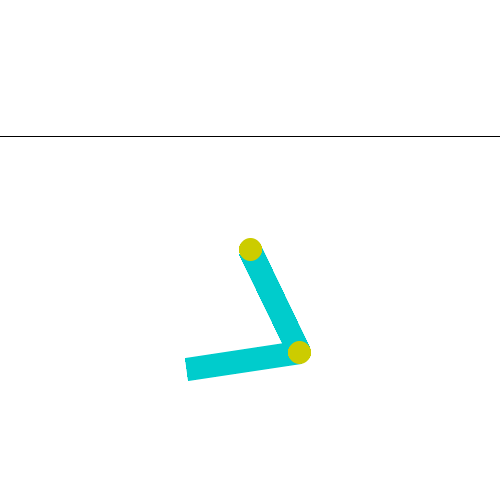
../../../_images/acrobot.gif

This environment is part of the Classic Control environments which contains general information about the environment.

Action Space

Discrete(3)

Observation Space

Box([ -1. -1. -1. -1. -12.566371 -28.274334], [ 1. 1. 1. 1. 12.566371 28.274334], (6,), float32)

import

gymnasium.make("Acrobot-v1")

Description

The Acrobot environment is based on Sutton’s work in “Generalization in Reinforcement Learning: Successful Examples Using Sparse Coarse Coding” and Sutton and Barto’s book. The system consists of two links connected linearly to form a chain, with one end of the chain fixed. The joint between the two links is actuated. The goal is to apply torques on the actuated joint to swing the free end of the linear chain above a given height while starting from the initial state of hanging downwards.

As seen in the Gif: two blue links connected by two green joints. The joint in between the two links is actuated. The goal is to swing the free end of the outer-link to reach the target height (black horizontal line above system) by applying torque on the actuator.

Action Space

The action is discrete, deterministic, and represents the torque applied on the actuated joint between the two links.

Num

Action

Unit

0

apply -1 torque to the actuated joint

torque (N m)

1

apply 0 torque to the actuated joint

torque (N m)

2

apply 1 torque to the actuated joint

torque (N m)

Observation Space

The observation is a ndarray with shape (6,) that provides information about the two rotational joint angles as well as their angular velocities:

Num

Observation

Min

Max

0

Cosine of theta1

-1

1

1

Sine of theta1

-1

1

2

Cosine of theta2

-1

1

3

Sine of theta2

-1

1

4

Angular velocity of theta1

~ -12.567 (-4 * pi)

~ 12.567 (4 * pi)

5

Angular velocity of theta2

~ -28.274 (-9 * pi)

~ 28.274 (9 * pi)

where

  • theta1 is the angle of the first joint, where an angle of 0 indicates the first link is pointing directly downwards.

  • theta2 is relative to the angle of the first link. An angle of 0 corresponds to having the same angle between the two links.

The angular velocities of theta1 and theta2 are bounded at ±4π, and ±9π rad/s respectively. A state of [1, 0, 1, 0, ..., ...] indicates that both links are pointing downwards.

Rewards

The goal is to have the free end reach a designated target height in as few steps as possible, and as such all steps that do not reach the goal incur a reward of -1. Achieving the target height results in termination with a reward of 0. The reward threshold is -100.

Starting State

Each parameter in the underlying state (theta1, theta2, and the two angular velocities) is initialized uniformly between -0.1 and 0.1. This means both links are pointing downwards with some initial stochasticity.

Episode End

The episode ends if one of the following occurs:

  1. Termination: The free end reaches the target height, which is constructed as: -cos(theta1) - cos(theta2 + theta1) > 1.0

  2. Truncation: Episode length is greater than 500 (200 for v0)

Arguments

Acrobot only has render_mode as a keyword for gymnasium.make. On reset, the options parameter allows the user to change the bounds used to determine the new random state.

>>> import gymnasium as gym
>>> env = gym.make('Acrobot-v1', render_mode="rgb_array")
>>> env
<TimeLimit<OrderEnforcing<PassiveEnvChecker<AcrobotEnv<Acrobot-v1>>>>>
>>> env.reset(seed=123, options={"low": -0.2, "high": 0.2})  # default low=-0.1, high=0.1
(array([ 0.997341  ,  0.07287608,  0.9841162 , -0.17752565, -0.11185605,
       -0.12625128], dtype=float32), {})

By default, the dynamics of the acrobot follow those described in Sutton and Barto’s book Reinforcement Learning: An Introduction. However, a book_or_nips parameter can be modified to change the pendulum dynamics to those described in the original NeurIPS paper.

# To change the dynamics as described above
env.unwrapped.book_or_nips = 'nips'

See the following note for details:

The dynamics equations were missing some terms in the NIPS paper which are present in the book. R. Sutton confirmed in personal correspondence that the experimental results shown in the paper and the book were generated with the equations shown in the book. However, there is the option to run the domain with the paper equations by setting book_or_nips = 'nips'

Version History

  • v1: Maximum number of steps increased from 200 to 500. The observation space for v0 provided direct readings of theta1 and theta2 in radians, having a range of [-pi, pi]. The v1 observation space as described here provides the sine and cosine of each angle instead.

  • v0: Initial versions release

References

  • Sutton, R. S. (1996). Generalization in Reinforcement Learning: Successful Examples Using Sparse Coarse Coding. In D. Touretzky, M. C. Mozer, & M. Hasselmo (Eds.), Advances in Neural Information Processing Systems (Vol. 8). MIT Press. https://proceedings.neurips.cc/paper/1995/file/8f1d43620bc6bb580df6e80b0dc05c48-Paper.pdf

  • Sutton, R. S., Barto, A. G. (2018 ). Reinforcement Learning: An Introduction. The MIT Press.