Pendulum#

This environment is part of the Classic Control environments.Please read that page first for general information.
Action Space |
Box(-2.0, 2.0, (1,), float32) |
Observation Shape |
(3,) |
Observation High |
[1. 1. 8.] |
Observation Low |
[-1. -1. -8.] |
Import |
|
Description#
The inverted pendulum swingup problem is based on the classic problem in control theory. The system consists of a pendulum attached at one end to a fixed point, and the other end being free. The pendulum starts in a random position and the goal is to apply torque on the free end to swing it into an upright position, with its center of gravity right above the fixed point.
The diagram below specifies the coordinate system used for the implementation of the pendulum’s dynamic equations.
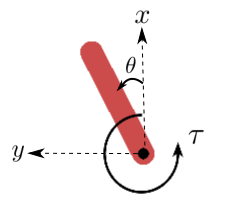
x-y: cartesian coordinates of the pendulum’s end in meters.theta: angle in radians.tau: torque inN m. Defined as positive counter-clockwise.
Action Space#
The action is a ndarray with shape (1,) representing the torque applied to free end of the pendulum.
Num |
Action |
Min |
Max |
|---|---|---|---|
0 |
Torque |
-2.0 |
2.0 |
Observation Space#
The observation is a ndarray with shape (3,) representing the x-y coordinates of the pendulum’s free
end and its angular velocity.
Num |
Observation |
Min |
Max |
|---|---|---|---|
0 |
x = cos(theta) |
-1.0 |
1.0 |
1 |
y = sin(theta) |
-1.0 |
1.0 |
2 |
Angular Velocity |
-8.0 |
8.0 |
Rewards#
The reward function is defined as:
r = -(theta2 + 0.1 * theta_dt2 + 0.001 * torque2)
where $ heta$ is the pendulum’s angle normalized between [-pi, pi] (with 0 being in the upright position).
Based on the above equation, the minimum reward that can be obtained is
-(pi2 + 0.1 * 82 + 0.001 * 22) = -16.2736044,
while the maximum reward is zero (pendulum is upright with zero velocity and no torque applied).
Starting State#
The starting state is a random angle in [-pi, pi] and a random angular velocity in [-1,1].
Episode Truncation#
The episode truncates at 200 time steps.
Arguments#
g: acceleration of gravity measured in (m s-2) used to calculate the pendulum dynamics. The default value is g = 10.0 .
import gymnasium as gym
gym.make('Pendulum-v1', g=9.81)
On reset, the options parameter allows the user to change the bounds used to determine
the new random state.
Version History#
v1: Simplify the math equations, no difference in behavior.
v0: Initial versions release (1.0.0)


